"There are three kinds of lies: lies, damned lies and statistics"
- attributed to Benjamin Disraeli (1804-1881) in Mark Twain, Autobiography, 1924, volume 1, page 246.

Basic statistics

In statistics, the term population is used to describe the entire collection of data to be analysed.
The entire population is often too large to deal with, so two means of handling this are random sampling or random assignment.
In random sampling, a sub-set of the population is assumed to be representative of the whole population and the observations are used to draw inferences about the whole population.  The chosen sub-set should contain the full range of characteristics of the population otherwise any analysis will only be valid for the sub-set.
In random assignment, used when studying the effects of some treatment variable, it is important that the subjects to be treated are randomly assigned.  Otherwise some recurrent characteristic within the selected sub-set may over-ride the effects of the parameter being studied and compromise the validity of the experimental results.

• The range of the data set is the difference between the largest and smallest number in the set.
• The mean of the data set is its average
• the arithmetic mean is the sum of all the values divided by the number of values
• the geometric mean is the square root of the product of two values, √(a.b), or n-th root of the product of n values
• for values of "2" and "200", the arithmetic mean is 101, but the geometric mean is 20.
• The median is the number which is in the exact middle of the data set when the data is arranged from the smallest to largest number.
• The mode is the number that appears the most often

In order to quantify any effect we need to collect data appropriate to the problem to be analysed.  For example, if we take all the one pound coins in the room and plot a histogram of their distribution against the issue date, it will appear as a ragged bar-chart starting in 1983 (before that we had one-pound notes) with gaps with no coins found for 1998/99 (unless it is from another state, e.g. Gibraltar).  But if we know how many pound coins were minted in each year, we can calculate the proportion of those coins for each year.  If we have a statistically meaningful sample, then the respective proportions should be close to the same number.  We could undertake a similar analysis in respect of the design on the reverse or the inscription on the edge.  The official figures for the number of one- and two-pound coins can be found on the Royal Mint website:

This Excel spreadsheet will help us to visualise the data collected for coins in this survey as a histogram: a chart with bars that represent numbers of observations within certain ranges (bins) of values.

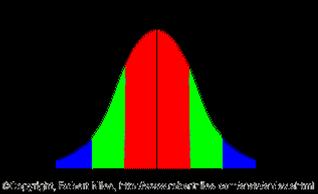
When a set of data corresponds to components made with a specific target value, there will often be a degree of variability around the mean.  The standard normal distribution is the most important continuous probability distribution. It was first described by De Moivre in 1733 and subsequently by the German mathematician Gauss (1777 - 1885). Normal distributions are a family of distributions with a symmetrical bell shape.  Most of the values occur in the middle of the curve and the area under each of the curves is the same:

The width of the curve is quantified as the standard deviation, s, of a normal distribution.  In Excel there are two different ways of deriving a standard deviation:

• STDEV: estimates the standard deviation based on a sample, using the following formula:
  
• STDEVP: calculates the standard deviation based on the entire population, using the following formula:
  

• One standard deviation from the mean (red area on the above graph) = ~68% of the area.
• Two standard deviations from the mean (the red and green areas) = ~95% of the area.
• Three standard deviations (the red, green and blue areas) = ~99% of the area.
  • Figure from RobertNiles.com/Statistics/Standard Deviation

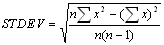
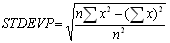
The variance is the square of the standard deviation, s².

Another useful graphical technique is a Pareto chart: a bar chart where data is presented with the number of occurrences (or frequency) on the y-axis.  The data is sorted such that whatever occurs most frequently is plotted on the left and whatever occurs least frequently is plotted on the right.  In consequence, the bar lengths reduce from left to right.  Vilfredo Pareto (1848-1923) was an economist who established that 80% of the land in Italy was owned by 20% of the population and subsequently realised that this principle was valid in other parts of his life.  It is now often referred to as the 80/20 rule.  The Pareto chart is especially useful for determining those defects which occur most often in products or processes and hence indicating where remedial effort would be best expended.  The Pareto principle can be applied to quality improvement as the majority of problems (80%) are produced by a few key causes (20%).

• Central tendency (mean, median and mode)  (StatsDirect Limited)
• Variance, standard deviation and spread  (StatsDirect Limited)
• Histogram  (StatsDirect Limited)
• Normal distribution  (StatsDirect Limited)
• Control plot  (StatsDirect Limited)
• Elementary concepts in statistics  (StatSoft Inc)
• Elementary statistics tutorial page  (Bobby Winters, Pittsburg State University)
• Statistical Methods for Psychology  (course notes corresponding to Chapters in the textbook by David C. Howell)
• StatisticalHelp.
• 5S Study and Research Page  (Creative Safety Supply  research and education center)
• Pareto chart  (Six Sigma)

SIX SIGMA (Evans & Lindsay pp 595-602)

Six-Sigma is an approach to measuring and improving product and service quality credited to Bill Smith, a reliability engineer at Motorola, in the 1980s, who:

• identified system failure rates were substantially higher than predicted by final product test
• suggested several causes, including
  •  high system complexity resulting in more opportunities for failure
  • fundamental flaws in traditional quality thinking
• concluded that much higher level of internal quality was required

In 1987, Motorola set the following goals:

• improve product and services quality ten times by 1989, and at least one hundred fold by 1991.
• achieve six-sigma capability by 1992
• with a deep sense of urgency, spread dedication to quality to every facet of the corporation,
  and achieve a culture of continual improvement to assure total customer satisfaction.
• "There is only one ultimate goal: zero defects - in everything we do".

Six Sigma is a measure of quality that strives for near perfection - that the process has less than 3.4 defects per million opportunities.  As the name indicates, the number of defect free operations corresponds to the area within ± six standard deviations (one standard deviation is denoted by sigma: σ) on a normal distribution curve. Six Sigma is a disciplined, data-driven approach and methodology for eliminating defects in any process or service activity.  A Six Sigma defect is defined as anything outside of customer specifications [Source].

Evans & Lindsay Slides 12-17: Means shifted by 1.5 SD

In Six-Sigma, a defect is any mistake or error that is passed on to the customer (i.e. a nonconformance).  Output quality then becomes

defects per unit (DPU) = number of defects discovered/number of units produced

although this definition appears too focussed on the final product rather than the process by which the product is generated.  An alternative definition for quality performance is:

defects per million opportunities (DPMO) = DPU * 1 000 000/opportunities for error

and hence Six-Sigma quality equates to a maximum of 3.4 DPMO.  In terms of the normal distribution, this can be visualised as three separate normal distributions with the respective means at -1.5σ, on target and +1.5σ such that the process mean only needs to be controlled within the range of the lower and upper mean to achieve Six-Sigma quality.  If the process mean were always on the target mean, then only 2 defects per billion operations would be expected.

Six-sigma quality corresponds to a process variation equal to half of the design tolerance.  Other quality levels can be defined such that the sigma-level is the distance from the target to the lower or upper specification limit (half the tolerance), hence for k-sigma quality:

k = tolerance/(2 * process standard deviation)

Now we can define a process capability index, C_p, sometimes called the process potential index:

C_p = the specification width/the natural tolerance of the process = (upper tolerance limit-lower tolerance limit)/6σ

which value of which increases with reduction of the spread (i.e. of the standard deviation). For k-sigma quality, C_p = 2kσ/6σ =k/3 and hence the value is 2 for six sigma quality or 1 for three sigma quality.  A quality level of 3.4 DPMO can be achieved with different shifts between the upper and lower means combined with changes in the quality level:

• 1.5σ off-centre and six-sigma quality
• 1.0σ off-centre and 5.5-sigma quality
• 0.5σ off centre and five-sigma quality

A change from three- to four-sigma quality represents a 10-fold improvement, from four- to five sigma a 30-fold improvement, and from five- to six-sigma a 70-fold improvement.

No process can be maintained in perfect control:
    Six-Sigma quality allows a shift of 1.5 standard deviations from the target mean value.
    If the target could be held, the expectation would be just 2.0 defects per billion operations.

General Electric [Evans & Lindsay p 599] used the Six-Sigma concept to achieve:

• a ten-fold increase in the life of x-ray tubes for computer tomography,
• a 400% improvement in return-on-investment in its industrial diamond business,
• a 62% reduction in turnaround time at railcar repair shops, and
• US$ 400M savings in its plastics business.

Citibank [Evans & Lindsay p 599]:

• reduced internal callbacks by 80%,
• reduced credit process times by 50%,
• reduced statement processing times by 46% (from 28 to 15 days).

The core philosophy of Six-Sigma is based on:

• DPMO as a standard that can be applied to all parts of an organisation
• extensive training and project team development
• corporate sponsors to support team activities
• creating highly-qualified process improvement experts
• use of appropriate metrics early in the process
• setting stretch objectives for improvement

At General Electric, a recognised benchmark for industry, the Six-Sigma approach uses DMIAC (a five phase problem solving approach) [Evans and Lindsay page 600]:

• D: Define
  • identify the customers and their priorities.
  • use business objectives, with customer requirements and feedback, to define a project.
  • identify characteristics that are critical-to-quality (CTQ).
• M: Measure
  • consider how the process is performing and how to measure that performance.
  • identify the key processes that influence CTQ characteristics.
  • measure the defects resulting from each of the key processes.
• A: Analyse
  • determine the most probable causes of the defects.
  • understand what variables are creating the process variation.
• I: Improve
  • seek means to remove the causes of defects.
  • confirm which parameters are affecting CTQ and to what extent.
  • identify acceptable ranges for key variables.
  • develop a system for measuring deviations of those key variables.
  • modify the process so that it remains within the acceptable range.
• C: Control
  • determine how to keep the improved system in place.
  • implement tools to ensure the variables remain with the required range.

The key differences to other Total Quality Management approaches are the use of statistical methodologies and the emphasis on customer requirements.  The key principles necessary for effective implementation of Six-Sigma are:

• committed leadership from top management.
• integration with existing initiatives, business strategy and performance measurement.
• process thinking.
• disciplined customer and market intelligence gathering.
• a bottom-line orientation (real savings or revenues in both the short- and long-term.
• leadership in the trenches (champions; master black, black and green belts; team members).
• training.
• continuous reinforcement and rewards.

URLs for Six-Sigma (checked as live on 24 July 2014):

• ASQ Six Sigma Forum.
• The Essence of Six Sigma (Breakthrough Management Group on YouTube).
• What is Six Sigma? (iSixSigma on YouTube)

Books on Six Sigma

• J Antony, A Kumar and R Banuelas, World Class Applications of Six Sigma, Elsevier, April 2006. ISBN13: 9780-7506-6459-2.  PU CSH Library.
• J Bicheno, Quality 75: towards Six Sigma performance in service and manufacturing, Picsie Press, 2002.  PU CSH Library.
• S Taghizadegan, Essentials of Lean Six Sigma, Elsevier, July 2006, ISBN13: 9780-12-370502-0.  PU CSH Library.
• G Tennant, Design for Six Sigma: launching new products and services without failure, Gower, Aldershot, 2002.  PU CSH Library.