Powerpoint Presentation (383 KB)

• Brainstorming
• Mind maps
• Cause-and-Effect (fishbone) diagrams.
• Failure Modes and Effects Analysis (FMEA).
• Fault Tree Analysis (FTA).
• Design of Experiments.

BRAINSTORMING (to follow)

MIND MAPS (to follow)

CAUSE AND EFFECT DIAGRAMS (Evans & Lindsay pp 614-616)

The Cause-and-Effect diagram (often referred to as a fishbone diagram or Ishikawa diagram) was introduced by Kaoru Ishikawa as a simple graphical method to record and classify a chain of causes and effects in order to resolve a quality problem.  A Cause-and-Effect diagram can be simply prepared by following just four steps [reference 1 citing the QC Handbook by Komatsu Limited]:

• Clarify the object effect
• a numerical measurement should be established against which subsequent improvement can be judged
• Pick causes
• create a team of people to brainstorm possible causes that may lead to the effect
• study the actual effect in the problem environment
• on a horizontal line draw diagonal branches for direct causes of the effect
• using arrows onto the branches create sub-branches for appropriate secondary causes
• confirm all elements of the diagram are correctly positioned
• quantify the causes wherever possible
• Determine the priority causes
• analyse any existing data for the problem
• if practical, create a Pareto diagram.  Otherwise, determine a ranking of the relative importance of each cause.
• Work out the counteractions for priority causes
• put in place appropriate solutions to eliminate or reduce the causes of problems

Image from http://www.ifm.eng.cam.ac.uk/dstools/gif/ishika.gif

Reference

1. HM Wadsworth, KS Stephens and AB Godfrey, Modern Methods for Quality Control and Improvement - second edition, Wiley, 2002.  ISBN 0-471-29973-1.

FAILURE MODE AND EFFECTS ANALYSIS (FMEA) (Evans & Lindsay pp 778-779)

Failure Mode and Effects Analysis is:

• a useful tool for reliability analysis
• systematic check of a product or process
  - function
  - failure causes
  - failure modes
  - failure consequences
  

FMEA requires a thorough knowledge of

• functions of the components
• contribution of those components to function of the system

For every failure mode at a low level, failure consequences are analysed at

• the local level
• the system level

FMEA is usually qualitative but may also be quantitative
FMEA is normally initiated during planning and definition of a project to investigate qualitative reliability demands of the market
FMEA is used during design and development, for quantitative reliability activities

FMEA can be used for design reviews

• definition and limiting of the system
• choice of complexity level
• check of component functions
• check of system functions
• identification of possible failure modes
• identification of consequences of failures
• possibility of failure detection and failure localisation
• assessment of seriousness of failure
• identification of failure causes
• interdependence of failures
• documentation

In quantitative design, FMEA may become Failure Mode, Effects and Criticality Analysis (FMECA)

• consider every component
• quantify and rank different failure modes
  

  F = probability of failure
  A = seriousness (consequences of failure)
  U = probability of non-detection before the product or service reaches the customer

• each parameter quantified by subjective judgement on a scale of 1-5 or 1-10
• Risk Priority Number (RPN) = F*A*U

It is perhaps easier to remember this in the form used in the motor industry: Severity, Occurrence and Detection (SOD instead of AFU)

Process-FMEA for may be used for

• pre-production engineering
• design of process control
• process improvement

Evans & Lindsay Slide 15: household lamp FMEA

URLs for Failure Mode and Effects Analysis (FMEA) (checked as live on 24 January 2005):

• Failure Modes and Effects Analysis (Competitive Edge Resources)
• Failure Modes and Effects Analysis (Pat Hammett)
• Failure Modes and Effects Analysis (RR Mohr - Jacobs Sverdrup)
• FMEA Info Centre
• Failure Modes and Effects analysis (Kinetic LLC)
• Incorporating a user-focussed FMEA-like technique into the design of safety critical systems (Jason Good and Ann Blandford)
• Risk–Informed Regulation of Marine Systems Using FMEA (Robb Willcox - USCG)

For more complex failures, FMEA may be supplemented by ...

FAULT TREE ANALYSIS (FTA) (Evans & Lindsay pp 779-780)

FTA is a logical chart of occurrences to illustrate cause and effects.
FTA was developed by DF Haasl, HA Watson, BJ Fussell and WE Vesely initially at Bell Telephone Laboratories then at North American Space Industry.

The common symbols used for FTA charts are:

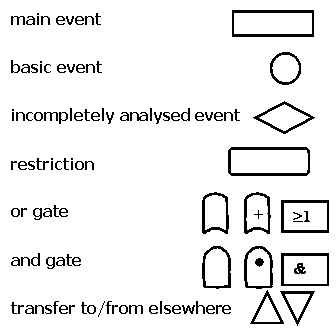
URLs for Fault Tree Analysis (FTA) (checked as live on 24 January 2005):

• Fault Tree Analysis (IEE Health and Safety Briefing 26c, September 2004)
• Fault Tree Analysis (NASA Lewis Research Center)
• Fault Tree Analysis (PL Clemens, Jacobs Sverdrup, February 2002)
• Fault Tree Analysis (Texas Workers' Compensation Commission)
• Fault Trees and Reliability Block Diagrams (weibull.com)
• Center for System Reliability (Sandia National Laboratory)
• Fault Tree Analysis programs (University of Maryland)

DESIGN OF EXPERIMENTS (Evans & Lindsay pp 530-534)

Design of Experiments was originally conceived by Ronald Aylmer Fisher at Rothampstead Experimental Station in Hertfordshire during the 1920s where he was analysing plant growing plots under different conditions and needed to eliminate systematic errors. Fisher devised a systematic application of latin and graeco-latin squares to the design of experiments.  Latin and Graeco-Latin squares and their application are described in detail at Tony Phillips' Latin Squares in Practice and in Theory I1 - I2 - I3 - I4.  A designed experiment enables the experimenter to compare two or more methods to determine which is better or to determine the effects of different levels of controllable factors in order to optimise the yield of a process or minimise the variation due to a response variable.

In cases where a number of factors may influence the output of a process, it may be possible to study all combinations of levels of each factor (a full factorial experiment), but if the number of factors to be considered increases then the number of experiments required increases more rapidly.  For two levels of n-variables, the number of experiments required is 2ⁿ, i.e. 4 experiments for two variables (low-low, low-high, high-low and high-high) or 16 experiments for four variables or 64 experiments for six variables.  Obviously if three levels (low - normal - high) or more are to be studied, then even more experiments are required and solving the problem with a full factorial experiment soon becomes impractical.  The results can be plotted to indicate the influence of each of the factors studied.  How the change in level of one factor affects the response is known as a main effect.  where there exists an interdependence between factors affecting the response, this is termed an interaction.

Genichi Taguchi developed orthogonal arrays (a fractional factorial matrix) that permits a balanced comparison of levels of any factor with a reduced number of experiments. In Taguchi design analysis, each factor can be evaluated independently of each of the other factors.  Taguchi's approaches have been used effectively by numerous companies, even though Evans and Lindsay (at page 534) suggest that the approach violates some traditional statistical principles, includes misleading analyses, ignores modern graphical approaches to data analysis and that he failed to advocate randomisation in performing the experiments.

URLs for Design of Experiments (checked as live on 25 January 2007):

Taguchi Designs (Carleton University)
Taguchi Design Tutorial (Design-Ease 6 User Manual)
NJA Sloane, A Library of Orthogonal Arrays
Orthogonal Arrays (Taguchi Designs)

Complementary teaching support materials:

• Evans and Lindsay chapter 9 Statistical Thinking and Applications
• Evans and Lindsay chapter 10 Quality Improvement
• Evans and Lindsay chapter 13 Reliability

RECOMMENDED TEXTS:

James Evans and William Lindsay, The Management and Control of Quality - Fifth Edition,
South-Western/Thomson Learning, Cincinnati OH, 2001.  ISBN 0-324-06680-5. PU CSH Library.
inc. CD-ROM with QuickTimeTM videos, web links and spreadsheets. ISBN 0-324-06682-1.