First, a couple of definitions:
- rheology: the science of flow and deformation of matter
- viscosity: the ability of a fluid to resist a change in the arrangement of the molecules when under an applied strain or stress. The standard symbol for viscosity is the Greek symbol eta: η.
- dynamic viscosity: the force required to overcome internal friction. The standard symbol for dynamic viscosity is the Greek symbol mu: μ. The SI units are Pascal-seconds (Pa·s: identical to 1 kg·m−1·s−1) although the composites industry often uses cgs units: centiPoise (cP). There is a direct numerical equivalence between milliPascal-seconds and centiPoise (1 mPa·s = 1 cP).
- kinematic viscosity: the ratio of the viscous force to the inertial force where the latter is a function of the fluid density (ρ). The standard symbol for kinematic viscosity is the Greek symbol nu: η and the SI units are m2·s−1. although the parameter is often given in centiStokes (cgs units: 1 centiStoke is 1 mm2/s) Hence η = μ/ρ.
| Dynamic viscosity (mPa.s) |
Material or Condition |
Reference |
| 1.0020 |
Water at 20 °C |
Kaye & Laby [1] |
| <20 |
Cyclic Butylene Terephthalate (CBT) monomer at 180ºC |
Coll et al [2] |
| 100 - 300 |
initial viscosity for RTM/infusion polyester, vinyl ester or epoxy resins |
Dupont et al [3] |
| <200 - ~400 |
initial viscosity for vacuum infusion of polyester or vinylester resins |
Cocquyt [4] |
| 800 |
upper limit for viscosity in RTM |
Becker [5] |
| 1000 |
non-injection point (NIP) in RTM |
Pearce et al [6] |
| 588-3500 |
melt viscosity of PLLA |
Ouagne et al [7] |
| 1500 - 2000 |
Crystic® 329EPA Class 2 Fire Retardant isophthalic laminating resin |
Scott Bader data sheet, 02/13. |
| 2500 |
Crystic® 1035PALSE general prupose orthophthalic low-styrene emission spray-up or hand lamination resin |
Huntsman Australia data sheet, 01/03. |
| 7500 - 16500 |
dwell-time window for wet-laid vacuum bagged composites |
Stringer [8] |
| 100 000 |
limiting viscosity for film-stacking |
Riedel et al [9] |
| 100 000 - 1000 000 |
"preferred [thermoplastic] melt viscosity range for most forming processes" |
Cogswell [10] |
| 300 000 |
melt viscosity of PEEK polymer |
Cogswell [10] |
| 1000 000 |
limiting viscosity for co-mingled fibre processes |
Riedel et al [9] |
| 1000 000 000 000 000 |
vitrimer topology freezing transition temperature (1012 Pa s) |
Denissen et al [11] |

Figure 1: Melt viscosities and processing temperatures of various matrix materials for both reactive and melt processing.
Figure 13 of K van Rijswijk and HEN Bersee, Reactive processing of textile fiber-reinforced thermoplastic composites: an overview, Composites Part A: Applied Science and Manufacturing, March 2007, 38(3), 666-681.
Effect of temperature on viscosity
Second, as the temperature rises it causes increased motion of the atoms in a
polymer chain and thus the polymer becomes more fluid. For a thermoplastic
polymer, there is a direct and reversible relationship between temperature and
viscosity (assuming no change in the molecular weight of the polymer due to
further polymerisation or to degradation). For the individual components
in a thermosetting resin there should also be a similar reversible relationship
between temperature and viscosity, but this will not be true for the mixed
materials. A typical relationship for the variation of viscosity with
temperature would be:
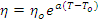 .................... (Equation 1)
.................... (Equation 1)
where η and T are the instantaneous viscosity and temperature respectively
and ηo is the viscosity at
temperature To. For a polyester resin, a typical value of a
would be -0.04ºC-1 which would result in:
- a 33% fall in viscosity for a 10ºC temperature rise,
- a
56% fall in viscosity for a 20ºC temperature rise, and
- a 70% fall in viscosity for a
30ºC temperature rise respectively [12].
Effect of cure on viscosity
Third, most thermosetting resins start out as a mixture of two low viscosity
components which react with one another to form a 3-D cross-linked network.
In consequence, the degree-of-cure and the viscosity increase with time after the mixing of the
components. This is normally accompanied by the generation of heat which will
act to accelerate the reaction. In the limit, this may result in smoke
and/or fire.
The heat evolved during cross-linking (cure) can be assumed to be proportional to the degree-of-cure of the resin
system with the equation to describe the reaction rate having the form: δα/δt = K(1-α)n where K is based upon the Arrhenius equation:
K = Ko.exp(-Ea/RT) and where:
- K is the overall reaction rate,
- Ko is the pre-exponential constant (per second)
- Ea is the activation energy (J/mol)
- R is the universal gas constant (J/mol.s), and
- T is the absolute temperature (K).
For resin systems cured by an addition reaction (e.g. polyester and vinyl
ester systems), the Kamal and Sourour [13] model is often used. It
incorporates both n-th order kinetics and an auto-catalytic term (Equation 2 [14]).
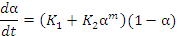 .................... (Equation 2)
.................... (Equation 2)
where:
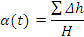
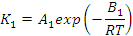
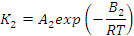
- ΣΔh is the cumulative specific heat release (J/kg),
- K1 and K2 are temperature dependent kinetic constants (per second)
- B1 and B2 are energy constants (J/mol)
- R is the universal gas constant (J/kg.K)
- T is the absolute temperature (K), and
- H is the specific enthalpy of reaction (J/kg)
For epoxy resin, White [15] modelled the PR286 resin system with the following
assumptions:
- the temperature of both the mould and the resin were equal,
- the problem could be simplified by considering it as a one-dimensional infinite plane problem,
- Equation 3 applies:
 .................... (Equation
3)
.................... (Equation
3)
where:
- η is the viscosity at temperature T and time t,
- ηo is the viscosity at time zero and is solely a function of temperature,
- log10(ηo) = 3.85E3/T(ºK)-8.93 is the rate of viscosity rise calculated from the constant temperature experiments, and
- log10(K(T)) = -3.93E3T(ºK)+8.66.
White further demonstrated that the profiles of the isothermal viscosity-time
curves of an epoxy resin system were identical when plotted on logarithmic axes.
The effect of temperature was a change in the position of the curve with respect
to those axes. The application of an appropriate shift along the
logarithmic time and logarithmic viscosity axes could bring any pair of curves
into coincidence. By implication, it follows that any isothermal
viscosity-time curve may be generated from any other by an appropriate scaling
of the time and viscosity axes.
Roller [16] presented experimental evidence for the applicability of Equation
4 for
the determination of the viscosity of curing B-staged epoxy resins as a function
of both time and temperature.
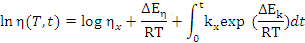 .................... (Equation
4)
.................... (Equation
4)
where:
- η is the time-dependent viscosity,
- ηo is the zero-time viscosity given by ηo = ηxeΔEη/RT, although this expression may not hold near (i.e. within 50ºC of Tg)
the glass transition temperature,
- ηx is the calculated viscosity of the material at
T=∞,
- ΔEη is the Arrhenius activation energy,
- k is the kinetic factor given by k = kxeΔEk/RT, where kx and ΔEk are the
analogues of η and ΔEη and the expression will not correctly model the
kinetics if the reaction mechanism changes within the temperature range
of interest,
- R is the gas constant, and
- t is time
In-process monitoring of viscosity: see the
Process Control webpage.
References
- Kaye and Laby Tables of Chemical and Physical Constants, http://www.kayelaby.npl.co.uk/general_physics/2_2/2_2_3.html, accessed 15 November 2007.
- S Coll, A Murtagh and C Ó Brádaigh, Resin Film Infusion of cyclic PBT composites: consolidation analysis, Proceedings of the Eighth International Conference on Flow Processes in Composite Materials, Newark (USA), 7-9 July 2004, pp 101-106.
- L Dupont, M Aguilar and A Poirier, An objective study of resin injection machines for resin transfer moulding of both low cost products and advanced composites, Proceedings of the 9th International Conference on Composite Materials (ICCM-9), Madrid, 12-16 July 1993. Woodhead Publishing, Cambridge UK, 1993, pp 489-496.
- A Cocquyt, The VIP (Vacuum Infusion Process) primer, GRPguru website, accessed at 17:14 on Wednesday 28 August 2013.
- DW Becker, Tooling for Resin Transfer Moulding, Wichita State University, Wichita – Kansas, no date.
- NRL Pearce, FJ Guild and J Summerscales, An investigation into the effects of fabric architecture on the processing and properties of fibre reinforced composites produced by resin transfer moulding, Composites Part A: Applied Science and Manufacturing, 1998, A29(1), 19-27.
- P Ouagne, L Bizet, C Baley and J Bréard, Analysis of the film-stacking processing parameters for PLLA/flax fiber biocomposites, Journal of Composite Materials, May 2010, 44(10), 1201-1215.
- LG Stringer, Optimization of the
wet lay-up/vacuum bag process for the fabrication of carbon fibre epoxy composites with high fibre fraction and low void content, Composites, 1989, 20(5), 441-452.
- U Riedel, J Nickel and AS Herrmann, High performance applications of plant fibres in aerospace and related industries, Fibres Seminar, IENICA, Copenhagen, 27 – 28 May 1999.
- FN Cogswell, Thermoplastic Aromatic Polymer Composites, Butterworth-Heinemann, Oxford, 1992. ISBN 0-7506-1986-7. PU CSH Library.
- W Denissen, JM Winne and FE Du Prez, Vitrimers: permanent organic networks with glass-like fluidity (minireview), Chemical Science, 2016, 7, 30-38.
- K Potter, Resin Transfer Moulding, Chapman & Hall, London, 1997. ISBN 0-412-72570-3. PU CSH Library.
- MR Kamal and S Sourour, Kinetics and thermal characterization of thermoset cure, Polymer Engineering and Science, January 1973, 13(1), 59-64.
- CD Rudd, AC Long, KN Kendall and CGE Mangin, Liquid Moulding Technologies, Woodhead Publishing, Cambridge, 1997. ISBN 1-85573-242-4. PU CSH Library.
- RP White, Time-temperature superpositioning of viscosity-time profiles of three high temperature epoxy resins, Polymer Engineering and Science,
January 1974, 14(1), 50-57.
- MB Roller, Characterization of the time-temperature-viscosity behaviour of curing B-staged epoxy resin, Polymer Engineering and Science, June 1975, 15(6), 406-414.
On-line resources:
Recommended reading:
The following books, where identified by [name], were suggested by contributors
to the
Biomimetics JISCmail discussion list:
- RB Bird and O Hassager, Dynamics of Polymeric Liquids: Volume 1 - Fluid Mechanics (second edition), Wiley, Bognor Regis, 1987. ISBN 0-471-80245-x
["THE reference - highly recommend chapters 2-3 as a start" - William Hartt]
- RB Bird, CF Curtiss, RC Armstrong and O Hassager, Dynamics of Polymeric Liquids: Volume 2, Kinetic Theory (second edition), Wiley, Bognor Regis, 1987. ISBN 0-471-80244-1.
- AH Cottrell, The Mechanical Properties of Matter, Wiley, London, 1964. UoP Library shelfmark 620.105 COT [Tony Atkins]. Also published by Krieger Publishing, 1981. ISBN 0-89874-168-8.
- PG DeGennes, Scaling Concepts in Polymer Physics, Cornell University Press, Ithaca NY, 1979. ISBN 0-8014-1203-x [Steve Eichhorn]
- DK Felbeck and AG Atkins, Strength and Fracture of Engineering Solids - second edition, Prentice Hall, 1996. ISBN: 0-13-856113-3. UoP Library shelmark 620.112 FEL. ["The obscure Deborah number is explained in simple terms" - Tony Atkins]
- RS Lakes, Viscoelastic Solids, CRC Press, Boca Raton FL, 1998. ISBN 0-84939-658-1 [William Hartt]
- RG Larson, The Structure and Rheology of Complex Fluids, Oxford University Press, Oxford, 1998. ISBN 0-19-512197-x [William Hartt].
- CW Macosko, Rheometry, Wiley-VCH, Weinheim, October 1994. ISBN 0-471-18575-2. UoP Library shelfmark 664.07MAC [William Hartt]
- Patrick Ostwald on "rheology" ? [Yves Brechet]
- RI Tanner and K Walters, Rheology: An Historical Perspective, Elsevier Rheology Series v7, 1988. ISBN 0-444-82945-8.
- IM Ward and J Sweeney, An Introduction to the Mechanical Properties of Solid Polymers - second edition, John Wiley & Sons, April 2004. ISBN 0-471-49626-x [Steve Eichhorn].
Return to MATS 347 home page
Created by John Summerscales on 02 February 2006 and updated on
16-Jan-2024 13:05. Terms and conditions. Errors and omissions. Corrections.



.................... (Equation 1)
.................... (Equation 2)
.................... (Equation 3)
.................... (Equation 4)